Visual intelligence information analysis

First of all, it is the problem analysis of problem C. The core idea of the problem is how to solve the distance between two points in the real scene according to the pixel distance on the image.

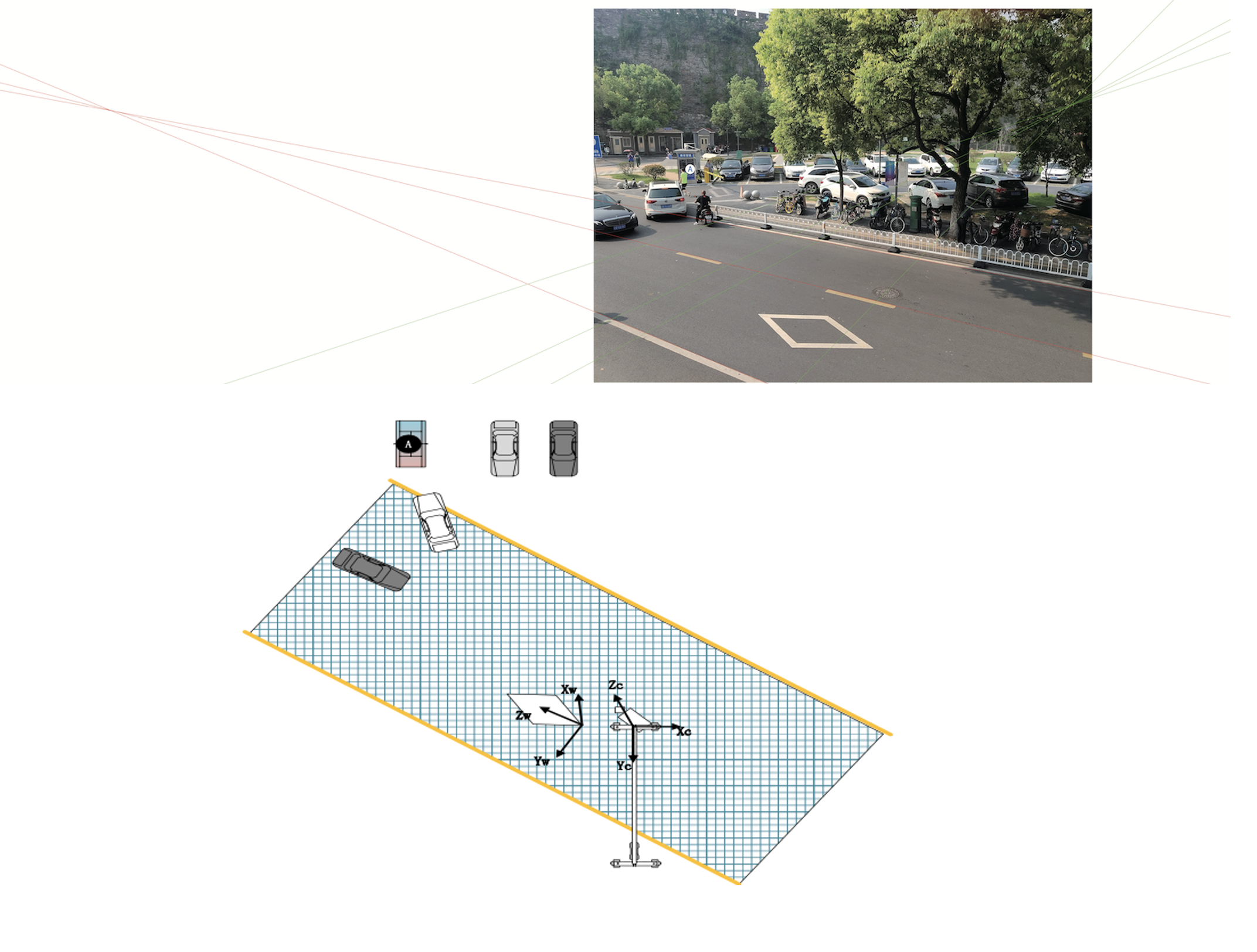
So, according to this core idea, here we choose the small hole imaging model to solve.

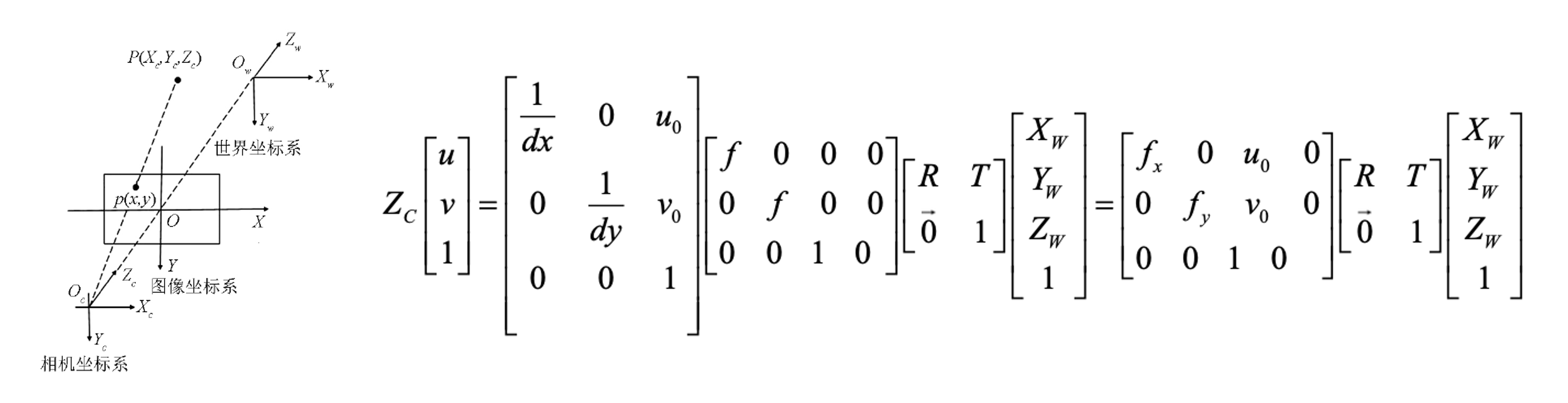
This model mainly describes the projection process of points in space on the image. In order to use this model to solve the problem, we need to solve the Euclidean transformation matrix, camera internal parameters and a normalized coefficient in the model.

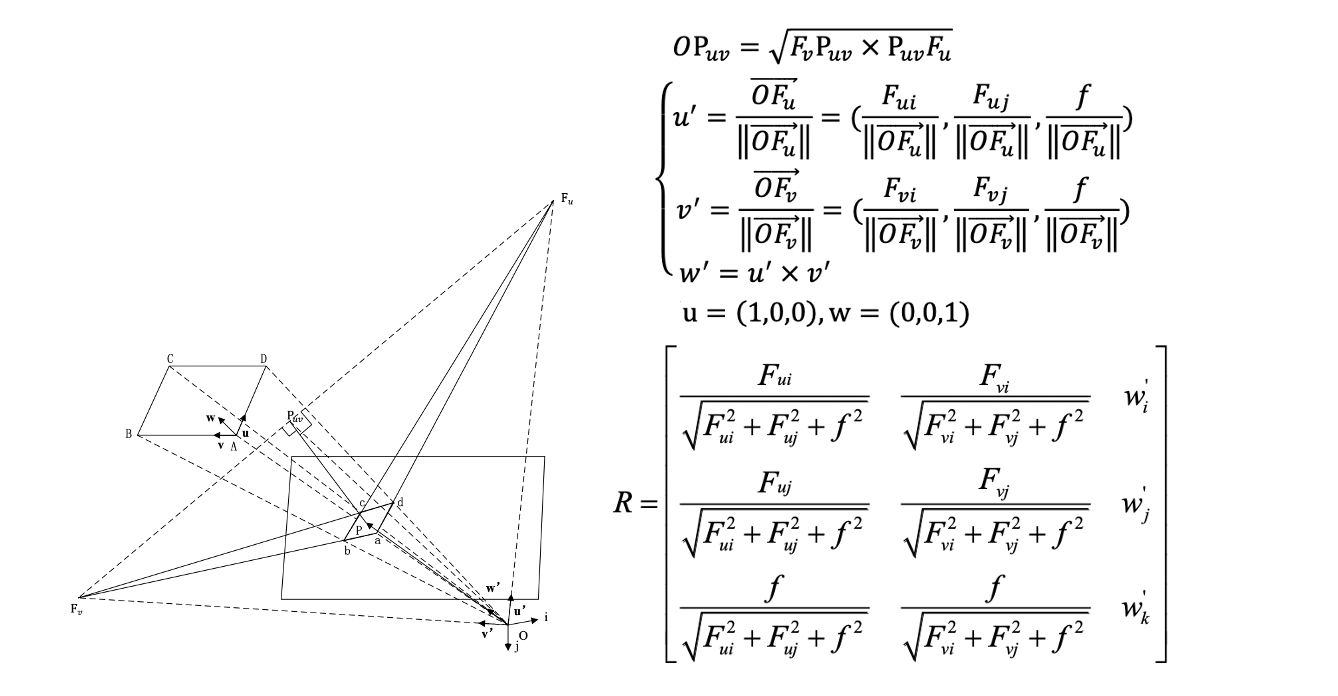
We choose the vanishing point equation of the camera to solve the rotation matrix of the camera and the focal length of the camera.

Then, according to the correspondence between the phase center, the vanishing point, the vanishing line and the parallel straight line in the real space in the image, the specific coordinates of the vanishing point can be used to solve the problem. Finally, according to the geometric projection relationship of a line segment vector with a clear distance in the real scene to the imaging plane, the translation matrix of the camera can be solved.

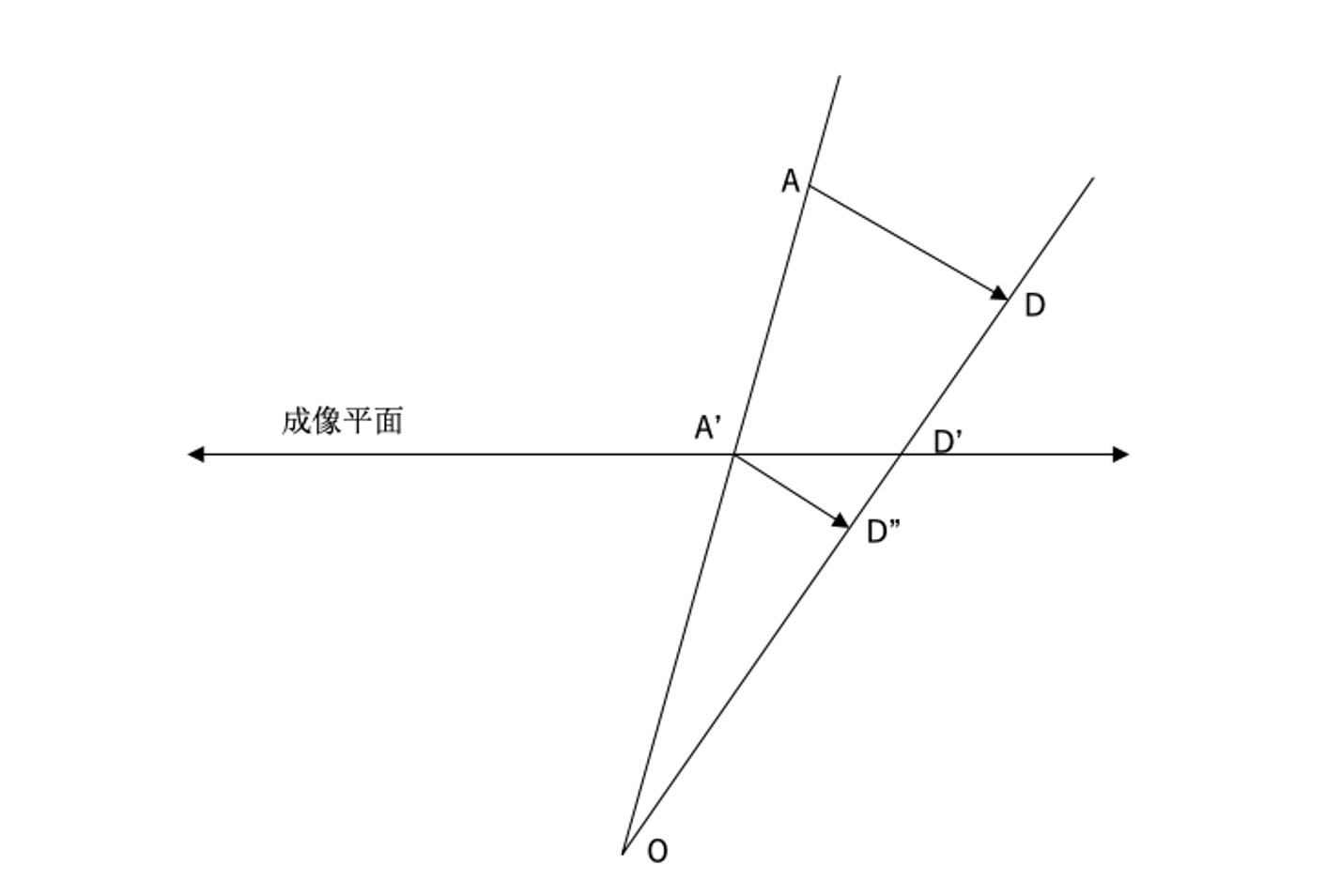
AD' is the projection of AD. Since the real length of AD is known, it is denoted as l, and there is AD_R0 in the world coordinate system, AD_RC in the camera coordinate system, and AD_RC = R·AD_R0. The straight line of AD intersects OD at point D'. With the help of the similar relationship between triangle OAD' and triangle OAD, we can get:

Through the above scheme, we can solve all the unknown coefficients in the small hole imaging model,

If you need to solve the specific coordinates of a point in the space plane, you only need to find the coordinates of the pixel point on the corresponding imaging plane and bring it into the publicity to get the space coordinates corresponding to this point.

After the small hole imaging model is constructed, all the problems described in the title can be solved according to this model. First find the vanishing point in the image to solve the rotation matrix of the camera, and then find a known distance in space to solve the translation matrix.

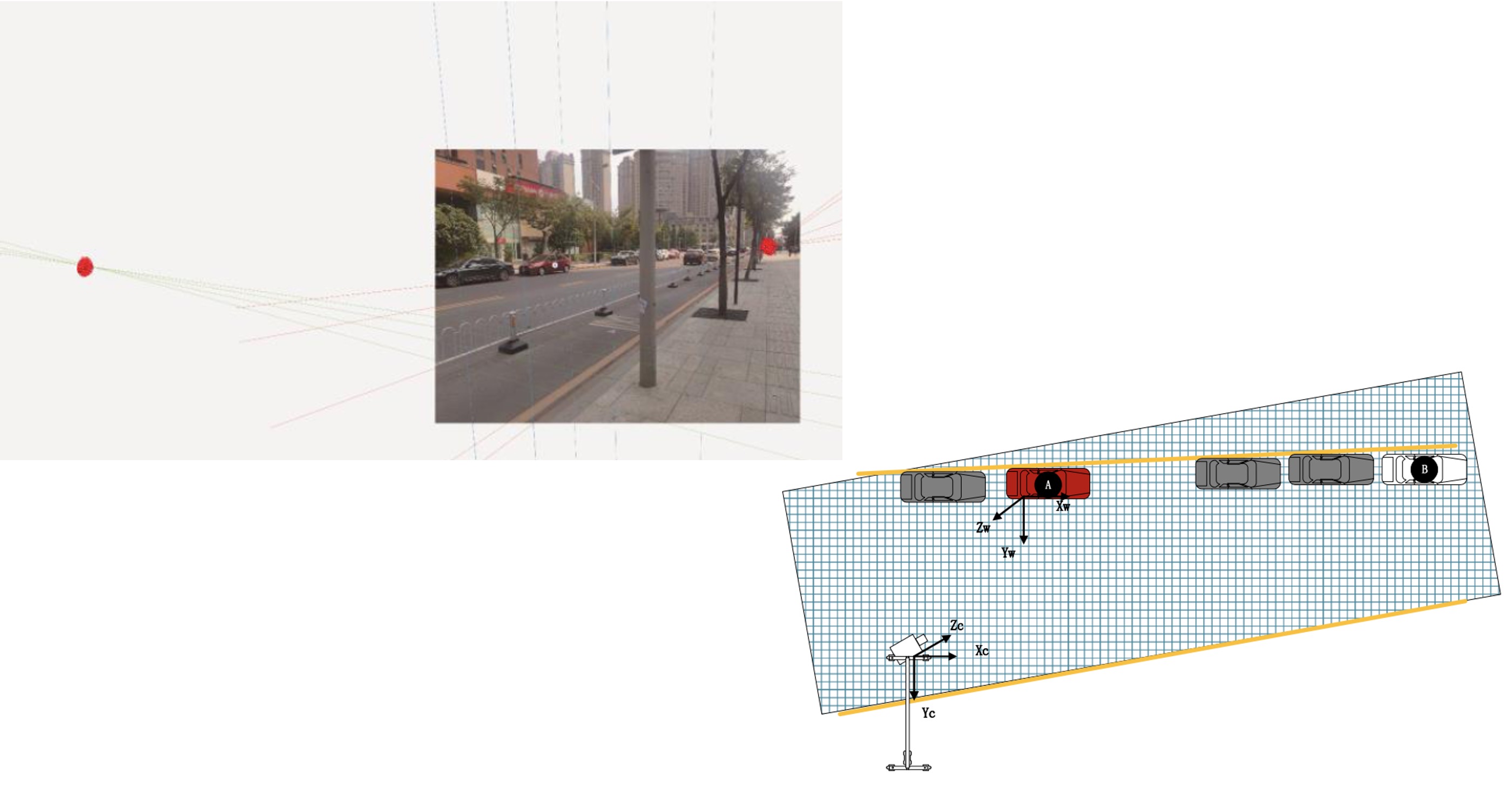
For Demo 1, the known distance we are looking for here is the wheelbase of this red hatchback Focus.

Then take the projection of the center axis of the Fox front wheel on the ground as the origin to construct the small hole imaging model.

Then if we ask to solve the spatial distance corresponding to any distance in the image, find the corresponding pixel and bring it in.

The known distance we selected for Demo2 is the front and rear wheelbase of this Cadillac XTS.

Demo3 selected this pedestrian crossing trailer.

For the following videos, we first use the SFM algorithm to obtain the pose relationship of the camera during the movement.

Then, in order to obtain the true pose of the camera that took the image, select the S-curve in a driving school training field that appeared in the first few frames as a true value distance, and then use the vanishing point and this true distance to solve the frame of the image. The rotation matrix and translation matrix in the real scene.

Finally, according to the absolute pose of this frame, the pose information of other cameras is reversed, and the distance information needed in the space is solved.

The manor issue is the same as above:

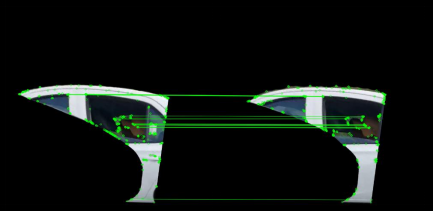
For the white car speed problem, we use the two-dimensional code posted on the shared car to transform the car image to a position parallel to the camera.

Use feature point method for image stitching and speed calculation

Use the rectified pictures for stitching and combine the dimensions of the real vehicle to get the transformation ratio difference from the image coordinate system to the real coordinate system.